In this article, you will learn about the Wheatstone Bridge and its working principles with some examples of circuits and applications.
Introduction
As we know, the 21st century is the age of development and inventions of electronics, and signals are the primary source for the use of electronics and for making connections. Today you will learn about Wheatstone Bridge’s working principles and applications.
Now, what are signals?
Signals are the primary source of communication, and in this age of development and inventions, there are various types of signals: Resistance, Induction, and capacitance measure.
What is Resistance?
Resistance is an instrument like an industrial sensor that checks the temperature, strain, humidity, displacement, liquid level, etc. When change is produced in the value of Resistance, it’s equivalent to the change in the receptive quantity. Hence, it’s explained that Resistance is essential as a signal sensor.
For Example:
Light Dependent Resistor or LDR is the most straightforward device to mention in the example of Resistance. Hence, as the name suggests, LDR is a device whose resistance changes according to the light supplied or fallen on it.
TYPES:
The resistance Measurement is divided into three types:
- Low Resistance Measurement
- Medium Resistance Measurement
- High Resistance Measurement
When the resistance valve or measurement is between a few micro ohms and mili ohms, it’s considered low Resistance. If the measurement is between 1ohm to a few hundred of KΩ, then it’s considered a medium resistance Measurement, and examples are potentiometers, thermistors, regular Resistors, etc.
At last, the high resistance Measurement is between a few Mega Ohms to more than 100 Mega Ohms.
NOTE: These Resistance Measurements are usually used for research purposes, and For finding the medium valve resistance, different methods are used usually, but usually, the Wheatstone Bridge is used.
What is Wheatstone Bridge?
In popular electrical tools, Bridge networks or circuits are often used. Some of the electronic tools are Measurement circuits, transducer circuits, switching circuits, and oscillators.
The Wheatstone Bridge is the most common and most accessible Bridge network or circuit used for accurately measuring resistance. It’s also used in Transducers to measure quantities like Temperature, Pressure, Strain, etc.
Wheatstone Bridge is also used in such applications where the sensor measures slight changes in resistance. In Transducers, it is used to convert the change in resistance to a change in voltage. Mainly this Bridge is used within the combination of operational Amplifiers to be used in Industries for various transducers and sensors.
Examples:
1: Thermistor: The change in Thermistor resistance occurs when it’s subjected to a change in temperature.
2: Strain Gauge: When resistance is subjected to pressure, force, or displacements, its resistance changes.
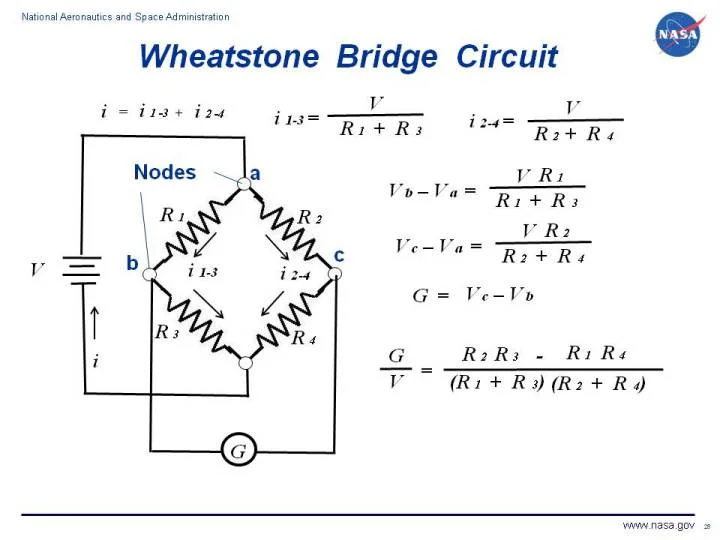
RESISTORS IN WHEATSTONE BRIDGE:
There are four resistors in Wheatstone Bridge, those are (R1, R2, R3, and R4) and all of these are connected in a diamond shape with the DC supply sources connected on the top and bottom of the circuit, and the output is taken from the other two ends ( A and B ). The diagram of the circuit is given below:
This Bridge is measured with the known resistance value to find the Unknown Resistance accurately. Indirectly, a Null or Balanced condition is used to find the unknown resistance through this Bridge.
In Balanced conditions, the output voltage of the Bridge at points A and B must be equal to 0. As compared to the above circuit:
VOUT = 0 V
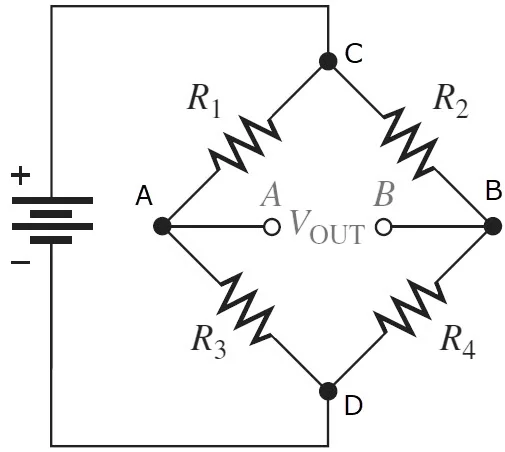
Let’s redraw the above circuit with more deals and clarity for a detailed study of the above circuit.
For finding the Unknown Resistance accurately this Bridge if used by measuring it with the known value of resistance. Indirectly, a Null or Balanced condition is used to find the unknown resistance through this Bridge.
In Balanced conditions, the output voltage of the Bridge at points A and B must be equal to 0. As compared to the above circuit:
VOUT = 0 V
For a detailed study of the above circuit, let’s redraw it with more deals and clarity.
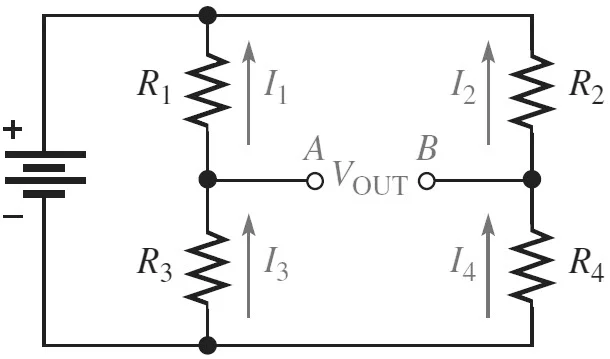
In the Balanced condition, the voltage between the resistors R1 and R2 is equal. If V1 is the voltage across R1 and V2 is the voltage across R2, then:
V1 = V2
Similarly, the voltage across resistors R3 (let’s name it V3) and R4 (let’s name it V4) are also equal. So,
V3 = V4
The voltage ratio can be written as:
V1 / V3 = V2 / V4
Ohm’s law is:
I1 R1 / I3 R3 = I2 R2 / I4 R4
Hence, I1 = I3 and I2 = I4, we get:
R1 / R3 = R2 / R4
From the above equation, it is clear that if we know the values of three Resistors, then it’s easy to find the value of the fourth one.
Alternative Way to Calculate Resistors:
In the redrawn circuit, if VIN is the input voltage, then the voltage at point A is:
VIN ( R3 / (R1 + R3))
Similarly, the voltage at point B is:
VIN ( R4 / (R2 + R4))
For the Bridge to be Balanced, VOUT = 0. But we know that VOUT = VA – VB.
So, in Balanced Bridge Conditions,
VA = VB
Using the above equations, we get the following:
VIN ( R3 / (R1 + R3)) = VIN ( R4 / (R2 + R4))
After simple manipulation of the above equation, we get:
R1 / R3 = R2 / R4
To find a conclusion from the above equation, if R1 is an unknown resistor, then its value can be calculated from the known values of R2, R3, and R4. Generally, the unknown value is known as RX and of the three known resistances, one resistor (primarily R3 in the above circuit is a variable Resistor called RV.
Find Unknown Resistance using a Balanced Wheatstone Bridge.
Let’s assume that R1 is an unknown resistor from the above circuit. So, it is known as RX. The resistors R2 and R4 have a fixed value. This means the ratio R2 / R4 is also fixed. Now, from the above calculation, the ratio of resistors must be equal to create a balanced condition i.e.
RX / R3 = R2 / R4
As the ratio R2 / R4 is fixed, we can easily adjust the other known resistor (R3) to achieve the above condition. Hence, R3 must be a variable resistor known as RV.
But here the question arises, How to make the Balanced Condition? Now Galvanometer (an old-school Ammeter) can be used by placing the Galvanometer between points A and B; then, we can detect the Balanced Condition.
With RX placed in the circuit, it adjusts the RV until the Galvanometer points to 0. At this point, note down the value of the RV. Using the following formula, you can calculate the unknown resistor value RX.
RX = RV (R2 / R4)
Unbalanced Wheatstone Bridge
If VOUT in the above circuit is not equal to 0 (VOUT ≠ 0), then the Wheatstone Bridge is known to be Unbalanced. PrimarilyThe Unbalanced Wheatstone Bridge is often used to measure physical qualities like Pressure, Temperature, Strain, etc.
In the case of transducers, it must be of a different resistive type, i.e., the resistance of the transducers changes accordingly when the quality of Temperature, strain, etc changes. Hence it proved that in place of the unknown resistor in the above resistance calculations, we can also connect the transducer.
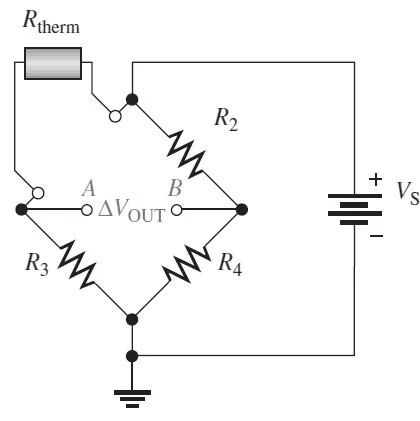
Wheatstone Bridge for Temperature Measurement
Let’s see how Temperature is measured using Wheatstone Bridge using a transducer, which is going to be used is known as Thermistor, which is a temperature-dependent resistor. Change in Temperature will either decrease or increase the Thermistor’s resistance as it depends on the nature of the thermistors.
From the above diagram, as a result, the output voltage of the Bridge VOUT will become a non-zero value. It means that the output voltage VOUT is proportional to the temperature. By calibrating the voltmeter, the temperature can be displayed
in terms of the output voltage.
Wheatstone Bridge for Strain Measurement
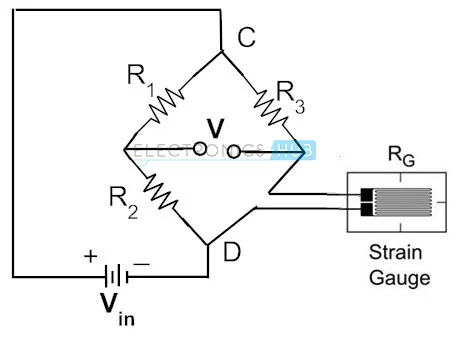
The most commonly used Wheatstone Bridge application is Strain Measurement. A strain gauge is a device whose electrical resistance is proportional to mechanical factors like Pressure, Force, or Strain.
The range of strain gauge resistance is mostly 30 Ω to 3000 Ω. In the diagram, the strain resistance may change only a fraction of the full range. So Wheatstone Bridge is used to measure accurately the fractional change of resistance.
The diagram shows a Wheatstone Bridge and the unknown resistor is replaced with a strain gauge.
The resistance of the strain gauge changes when an external force is applied, and the Bridge becomes Unbalanced as a result. The output voltage is calibrated to show the change in strain.
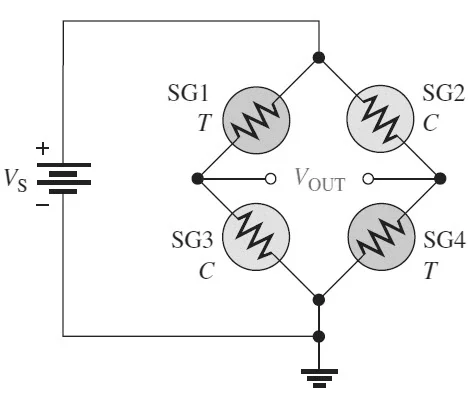
Weight Scale is one of the most popular applications of Strain Gauge and Wheatstone Bridge. In it, the Strain Gauge is carefully fixed as a single unit, known as Load Cell. A Load Cell transducer changes mechanical force to an electrical signal.
Mainly, the Weight Scale consists of four load cells. When an external force is applied, two strain gauges expand or stretch, and the other two are placed when the load is placed.
The strain gauge resistance depends on its situation; when it’s tensed or compressed, the change in resistance occurs either increased or decreased. As a result, the Bridge becomes Unbalanced, producing voltage indicator action on the voltmeter corresponding to the strain change.
The voltage difference is more significant across the strain gauge’s meter terminals if more strain is applied. The meter shows a zero reading if the strain is zero and Bridge is balanced.
The Wheatstone Bridge is usually used in strain gauges as it’s used for fractional Measurement of resistance. It’s about using Wheatstone Bridge for resistance Measurement for precise measurements.
Applications
- For studying shallow resistance values accurately, the Wheatstone Bridge is used.
- It’s also used for measuring the physical parameters like Temperature, Strain, light, etc. when placed next to the operational Amplifier.
- The variations on Wheatstone Bridge also help to measure quantities, capabilities, Inductance, and impedance.
Conclusion
It’s a guide for beginners. After reading this article, readers will be able to understand what’s Wheatstone Bridge is, How to Calculate an unknown resistance using Wheatstone Bridge, how to balance the Bridge and what situation makes it Unbalanced, and how physical quantities affect the Bridge.